Introduction aux SDR: 1ere partie

 Ce manuel est destiné à présenter des concepts rapidement et en douceur, permettant au lecteur d'exécuter DSP et d'utiliser les SDR intelligemment. Il n’est pas destiné à être un manuel de référence pour tous les sujets DSP / SDR; il existe déjà de nombreux excellents manuels, tels que le manuel SDR d'Analog Device et dspguide.com. Vous pouvez toujours utiliser Google pour rappeler les identités trigonométriques ou la limite de Shannon. Considérez ce manuel comme une passerelle vers le monde du DSP et du SDR: il est plus léger et moins coûteux en temps et en argent que les cours et manuels plus traditionnels.

 

Domaine des fréquences

L'un des effets secondaires les plus intéressants de l'apprentissage du DSP et des communications sans fil est que vous apprendrez également à penser dans le domaine des fréquences. L’expérience de la plupart des gens dans le domaine des fréquences se limite au réglage des boutons de graves / médiums / aigus du système audio d’une voiture. L'expérience de la plupart des gens en matière de visualisation de quelque chose dans le domaine de fréquence se limite à voir un égaliseur audio, tel que ce clip:

 

 

 

 

 Dans ce chapitre, nous couvrons ce que signifie le domaine fréquentiel, comment convertir le temps et la fréquence (plus ce qui se passe lorsque nous le faisons), et quelques principes intéressants que nous utiliserons plus tard. À la fin de ce manuel, vous serez un maître dans le domaine des fréquences, c'est garanti!

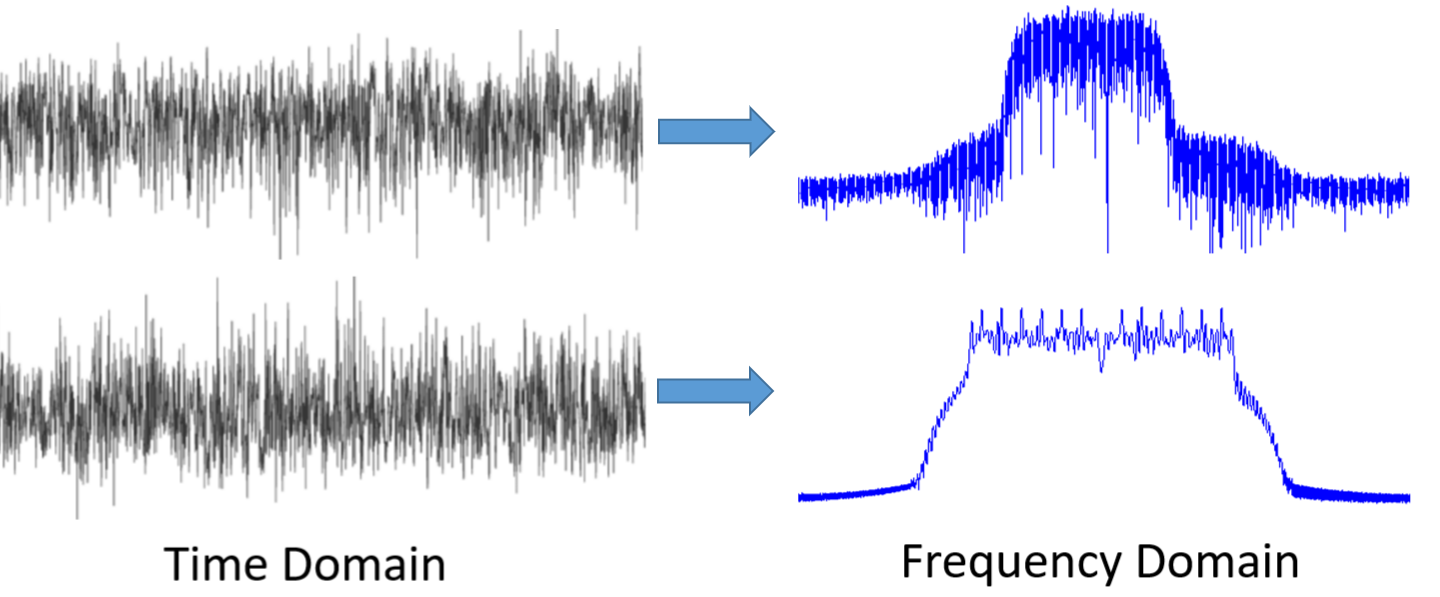
Premièrement, pourquoi aimons-nous regarder les signaux dans le domaine fréquentiel? Eh bien, voici deux exemples de signaux, affichés à la fois dans le domaine temporel et fréquentiel.

 

 

Comme vous pouvez le voir, dans le domaine temporel, ils ressemblent tous deux à du bruit, mais dans le domaine fréquentiel, nous pouvons voir différentes caractéristiques. Tout est dans le domaine temporel sous sa forme naturelle; lorsque nous échantillonnerons des signaux, nous les échantillonnerons dans le domaine temporel, car vous ne pouvez pas échantillonner directement un signal dans le domaine fréquentiel. Mais les choses intéressantes se produisent généralement dans le domaine des fréquences.
Série Fourier

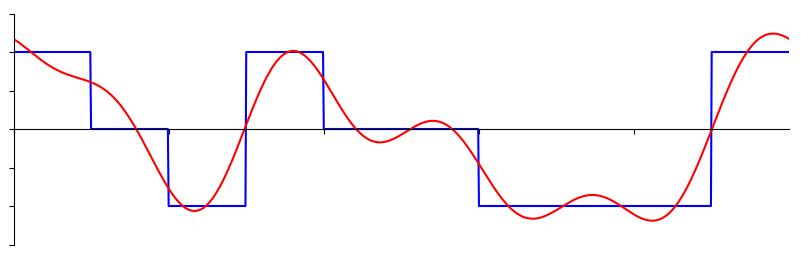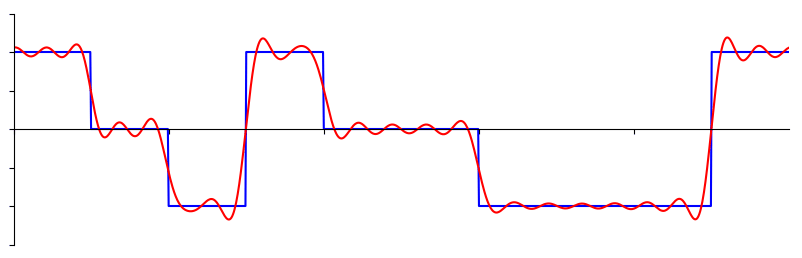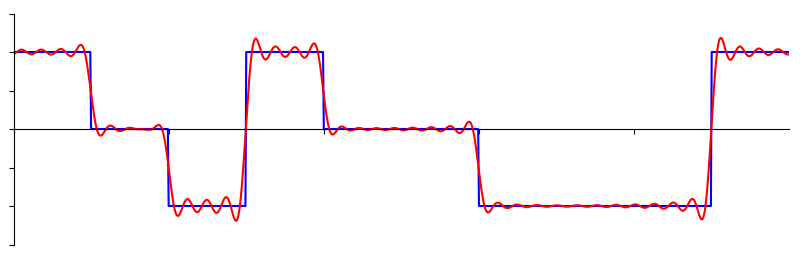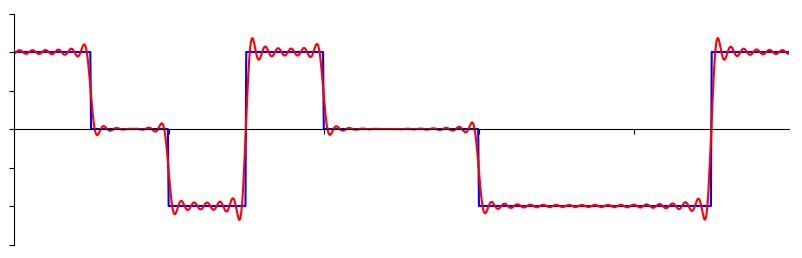
Les bases du domaine fréquentiel commencent par comprendre que tout signal peut être représenté par des ondes sinusoïdales additionnées. Lorsque nous décomposons un signal en ses ondes sinusoïdales composites, nous l'appelons une série de Fourier. Voici un exemple de signal composé de seulement deux ondes sinusoïdales:

Voici un autre exemple; la courbe rouge ci-dessous se rapproche d'une onde en dents de scie en additionnant jusqu'à 10 ondes sinusoïdales. Nous pouvons voir que ce n’est pas une reconstruction parfaite - il faudrait un nombre infini d’ondes sinusoïdales pour reproduire cette onde en dents de scie en raison des transitions brusques:

Certains signaux nécessitent plus d'ondes sinusoïdales que d'autres, et certains nécessitent une quantité infinie, bien qu'ils puissent toujours être approximés avec un nombre limité. Voici un autre exemple de signal décomposé en une série d'ondes sinusoïdales:

Pour comprendre comment nous pouvons décomposer un signal en ondes sinusoïdales, ou sinusoïdes, nous devons d'abord examiner les trois attributs d'une onde sinusoïdale:

     Amplitude
     Phase
     La fréquence

L'amplitude indique la «force» de l'onde, tandis que la phase est utilisée pour représenter la façon dont l'onde sinusoïdale est décalée dans le temps, de 0 à 360 degrés (ou de 0 à 2 \ pi). La fréquence est le nombre d'ondes par seconde.

À ce stade, vous avez peut-être réalisé qu'un «signal» n'est essentiellement qu'une fonction, généralement représentée «au fil du temps» (c'est-à-dire l'axe des x). Un autre attribut facile à retenir est la période, qui est l'inverse de la fréquence. La période d'une sinusoïde est la durée, en secondes, pour que l'onde termine un cycle. Ainsi, l'unité de fréquence est 1 / seconde, ou Hz.

Lorsque nous décomposons un signal en une somme d'ondes sinusoïdales, chacune aura une certaine amplitude, phase et fréquence. L’amplitude de chaque onde sinusoïdale nous indiquera la force de la fréquence du signal d’origine. Ne vous inquiétez pas trop de la phase pour le moment, si ce n'est de réaliser que la seule différence entre sin () et cos () est un décalage de phase (décalage temporel).

Il est plus important de comprendre le concept sous-jacent que les équations réelles à résoudre pour une série de Fourier, mais pour ceux qui s'intéressent aux équations, je vous renvoie à l'explication concise de Wolfram: https://mathworld.wolfram.com/FourierSeries.html.