Introduction aux SDR: 2 eme partie

 Paires temps-fréquence

Nous avons établi que les signaux peuvent être représentés sous forme d'ondes sinusoïdales, qui ont plusieurs attributs. Maintenant, apprenons à tracer des signaux dans le domaine fréquentiel. Alors que le domaine temporel montre comment un signal change au fil du temps, le domaine fréquentiel affiche la quantité de signal dans quelles fréquences. Au lieu que l'axe des x soit le temps, ce sera la fréquence. Nous pouvons tracer un signal donné en temps et en fréquence. Regardons quelques exemples simples pour commencer.

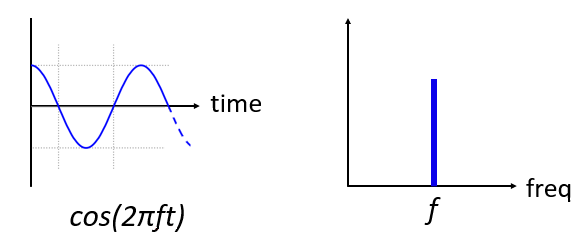
Voici à quoi ressemble une onde sinusoïdale, de fréquence f, dans le domaine temporel et fréquentiel:

Le domaine temporel doit paraître très familier. C’est une fonction oscillante. Ne vous inquiétez pas à quel moment du cycle il commence ou combien de temps il dure. Le résultat est que le signal a une seule fréquence, c'est pourquoi nous voyons un seul pic / pic dans le domaine fréquentiel. Quelle que soit la fréquence à laquelle l'onde sinusoïdale oscille, nous voyons le pic dans le domaine fréquentiel. Le nom mathématique d'un pic comme celui-ci est appelé «impulsion».

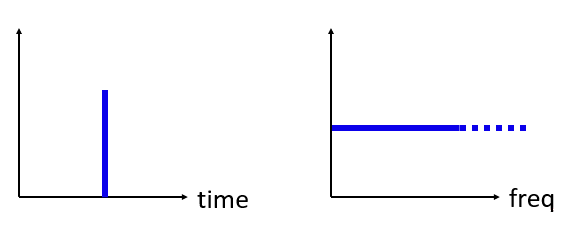
Et si nous avions une impulsion dans le domaine temporel? Imaginez un enregistrement sonore d'une personne applaudissant ou frappant un clou avec un marteau. Cette paire temps-fréquence est un peu moins intuitive.

Comme nous pouvons le voir, un pic / impulsion dans le domaine temporel est plat dans le domaine fréquentiel et contient théoriquement toutes les fréquences. Il n'y a pas d'impulsion théoriquement parfaite car elle devrait être infiniment courte dans le domaine temporel. Comme l'onde sinusoïdale, peu importe où dans le domaine temporel l'impulsion se produit. Ce qu'il faut retenir ici, c'est que des changements rapides dans le domaine temporel entraînent l'apparition de nombreuses fréquences.

Examinons ensuite les tracés du domaine temporel et fréquentiel d'une onde carrée:

This one is also less intuitive, but we can see that the frequency domain has a strong spike at 10 Hz, which is the frequency of the square wave, but it also seems to keep going. It is due to the quick change in time domain, just like in the previous example. But it’s not flat in frequency. It has spikes at intervals, and the level slowly decays (although it will continue forever). A square wave in time domain has a sin(x)/x pattern in the frequency domain (a.k.a. the sinc function).

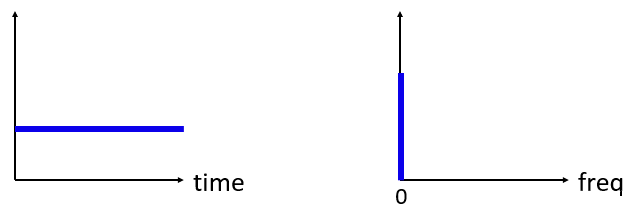
Now what if we have a constant signal in the time domain? A constant signal has no “frequency”. Let’s see:

Parce qu'il n'y a pas de fréquence, dans le domaine fréquentiel, nous avons un pic à 0 Hz. Cela a du sens si vous y réfléchissez. Le domaine fréquentiel ne sera pas «vide» car cela ne se produit que lorsqu'il n'y a pas de signal présent (c'est-à-dire, domaine temporel de 0s). Nous appelons 0 Hz dans le domaine fréquentiel "DC", car il est causé par un signal DC dans le temps (un signal constant qui ne change pas). Notez que si nous augmentons l'amplitude de notre signal CC dans le domaine temporel, le pic à 0 Hz dans le domaine fréquentiel augmentera également.

Plus tard, nous apprendrons ce que signifie exactement l'axe y dans le tracé du domaine fréquentiel, mais pour l'instant, vous pouvez le considérer comme une sorte d'amplitude qui vous indique la quantité de cette fréquence présente dans le signal du domaine temporel.